
Vocabulary acquisition and the learning curve. Proceedings of the National Academy of Sciences, 101(36), 13124-13131.ĭaller, M., Turlik, J., & Weir, I. The learning curve: implications of a quantitative analysis. The American journal of psychology, 64(3), 327-349. The learning curve in relation to other psychometric functions. If that first "trial" is a whole block then maybe this is not a terrible assumption, but that's mainly because you've already passed the peak slope of the sigmoidal function early on if you used the entire data then a sigmoid would still fit better.Ĭuller, E., & Girden, E. In most tasks without substantial prior instruction, you need at least a couple of trials to even figure out what is going on, and can't start to improve until then. With an exponential fit, you are supposing that the most learning occurs at the point of the first trial. Looking at the data you posted, the peak slope (peak of the first derivative) is probably a decent choice, although I'm not sure you really have enough data points in the first month to get a good measure.Įxponential fits are likely to be more unstable, and in the data you've posted it looks like your fit is overfitting the beginning and end of the learning process, so you're missing the most important part for determining the actual "speed", which is between your first 3 data points none of these are fit well. Which one is more applicable will depend on how learning in your paradigm varies across subjects and conditions. The time to peak and slope at peak are both parameters you can use to measure learning rate, though they measure somewhat different things. There are a variety of sigmoidal functions, but they are all differentiable and have a central peak in the first derivative. Importantly, learning is often not fastest at the start, there is often some level of "aha!" moment later on. Your exponential fits decently, but it probably doesn't describe the actual underlying process very well. Sigmoids are more general and probably better for modeling learning than a simple exponential. One-phase association Y=Y0 + (Plateau-Y0) (1-exp(-Kx)).

Diamonds: derived fitting features irrelevant to the question proper. Learning curve obtained in quiet at 65 dB speech level. * EDIT: after a literature search I found that the logit function is a sigmoid function, and, hence, it does have a slope parameterįig. Is a logit function the best way to fit a learning curve?* Afaik, a logit function does not have a slope parameter and hence, from my pov, it would be less fitting for my purposes (pun not intended).
#Graphpad prism 4 parameter logistic curve fit software#
The function I used I found in another software package called GraphPad Prism. I did this using regression analysis using the least-squares method in MATLAB. Now I seek to fit a function to these data, because I want to know how fast they learn. In the beginning they learn quick, and this levels off as to what seems a maximum (Fig.
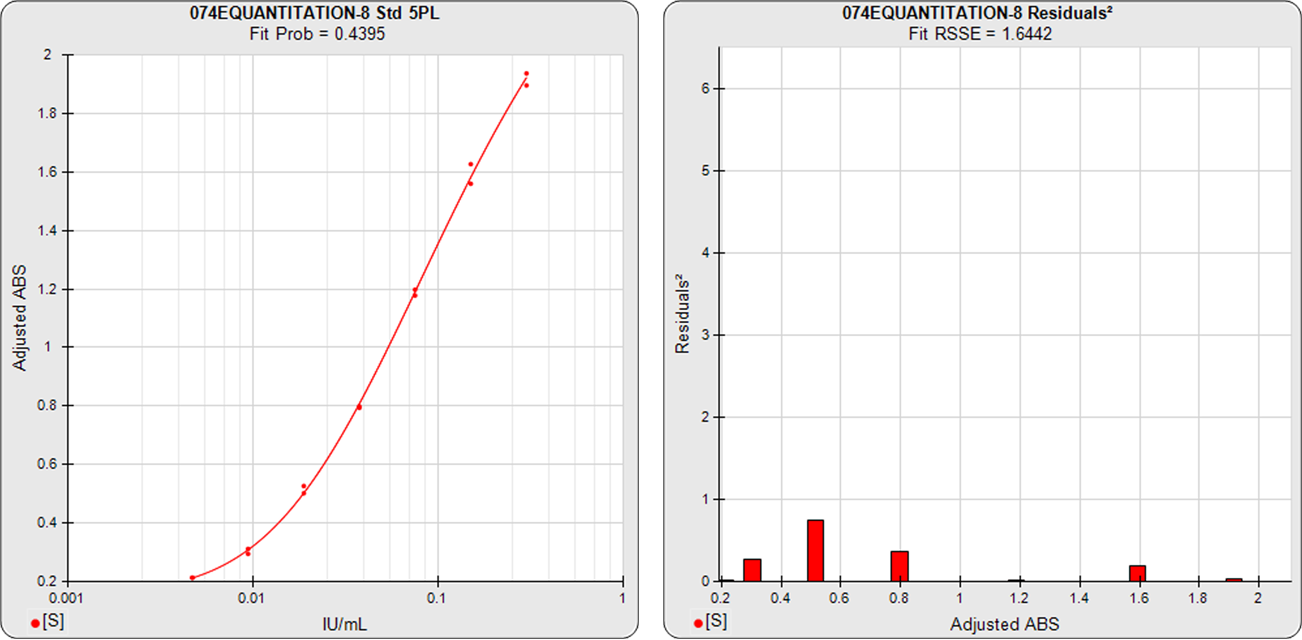
Typically, these learning curves start at a value around 25% and end at 80% (barred the rock stars, CI users never reach 100%). The %correct score runs from a minimum of 0%, to a maximum of 100%. The outcome measure of speech tests is a simple word or phoneme correct score. Along the way, speech recognition is tested frequently. These folks get a CI, and then need to start learning to understand speech again. I am fitting learning curves for cochlear implant (CI) users.


 0 kommentar(er)
0 kommentar(er)
